Az alapja minden olyan tanításnak, amely ismeri a világot matematika. Pontos tudomány használja hivatalos nyelv és megvizsgálja a kiválasztott absztrakt objektumok rendjét, felépítését és kapcsolatát. Nem minden tanulónak tetszik a matematika összetettség és zavar, de valószínűleg azért félreértés. A matematikával kapcsolatos tartós változások elkötelezettséget, koncentrációt, következetességet, még makacsosságot és - ami a legfontosabb - gyakorlati megoldásokat igényelnek. A tanulmányban fontos lépésről lépésre megérteni kezdetben az egyszerűséget, és fokozatosan lépni a komplexebbre, anélkül, hogy valamit érthetetlennek és rosszul átgondoltnak hagyna.
Számos különböző matematikai ága van, amelyeket kellően tanulmányoztak, és a közelmúltban megjelentek. Az alábbiakban leírjuk a matematikai elemzés alapjait - az alapvető fogalmakat, meghatározásokat és szabályokat az egy változó, derivál és differenciálás egyszerű funkcióinak tanulmányozására.
Az aforizmus az általános iskolások körében merült fel: "A matematika nagyon bonyolultá válik, amikor a szám eltűnik." Valójában közelebb kerülnek a matematikai tudományok néhány definíciójának és törvényének megértéséhez, amikor konkrét példák felhasználásával döntenek a szabályokról..
Főbb meghatározások
Kezdjük a terminológiával - az elsődleges meghatározások egyszerű általános szemantikai jelentéseivel:
- változó - érték vagy szimbólum, a számok bármelyike lehet
meghatározott terület (a gyermek súlya vagy magassága)
- függvény - a cél, a munka, a tevékenység, a konkrét hatása a változóra, f (x) -et (a gyermek súlyának függését a magasságától) jelöljük
- határ - határ, határ, él (horizont - látómező)
- derivált - kialakult, másodlagos, egy másikból áramló, f '(x) -et (sebesség mozogva) jelölünk
- differenciális - különbség, megkülönböztetés, szétválasztás.
A funkció igazságos
A függvény annak a következménye, amit egy változóval csinál, azaz számítási eredmény. Ez az elemek viszonya, amelyben az egyik változó megváltozása a másik megváltozását okozza. Ossza el az f (x) -t egyszerû és összetett részre.
A függőségek megjelenítésére a következő módszereket használjuk: algebrai, grafikus, táblázatos, logikai és akár szoftver.
A numerikus függőségeket algebrai módon határozzuk meg a változók, az egyenlőségek és az egyenlőtlenségek (≤ és>) szimbólumaival, és elkészítjük a forma egyenletét: y = f (x), itt x változó vagy argumentum, y vagy f (x) pedig egy függvény. Az elfogadható definíciós tartományból származó x változó minden egyes értékére egy adott f (x) y értékének felel meg..
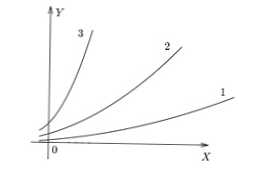
Az alábbi ábra egyszerű grafikonokat mutat, 3 különböző arányról. Látható, hogy f (x) 3-ban a y legnagyobb értékét x-specifikusra kapjuk, f (x) 1 -ben - a legkisebbet.
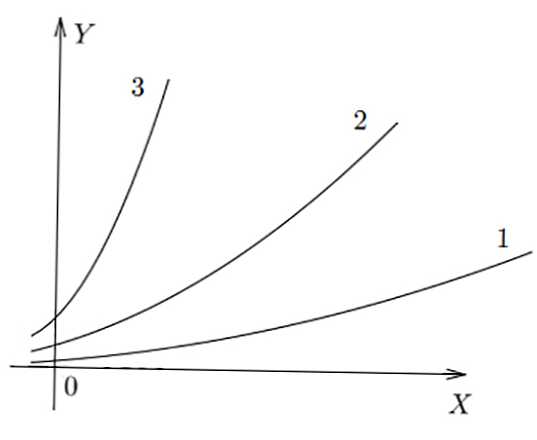
függvény
A következő elemi kifejezéseket különböztetjük meg: lineáris (közvetlen), kvadratikus (parabola), köbös, hiperbola, exponenciális, logaritmikus, trigonometrikus (az alábbi táblázatban látható).
Az f (x) típusok elemzéséhez meghatározzuk azok tulajdonságait (lásd alább), ehhez a származék és a differencia fogalmát használjuk..
Származékos funkció
derivált - operátor, amely az eredeti f (x) esetében a differenciálódási törvények szerint egy másik funkciót társít, jellemzi az x argumentum f (x) primer változását valamikor. Ennek részletesebb megértése érdekében a függőség és a differenciálódás határának összetettebb definícióival kell foglalkozni..
határ - ez a meghatározás dinamikus. Az x kifejezés n-re való hajlamát a következőképpen kell érteni: x olyan értékeket szerez, amelyek n közelében vannak, és apró különbséggel különböznek egymástól..
differenciális - valamilyen nagyságrendű kis változás. A növekményt delta-nak hívják.
Az f (x) deriváltja egy ponton az a pont, amikor a függvény delta-t elosztjuk a változó delta-val egy adott ponton, ha ez utóbbi 0-ra hajlamos.
Az adott ponton a függőség változásának sebessége, geometriailag megmutatható a függvényhez tartozó alfa dőlésszögének tan-értékével.
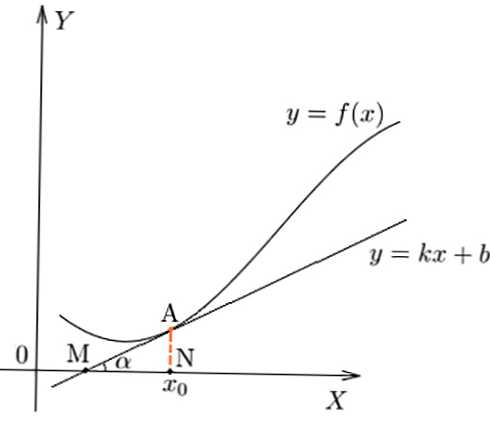
derivált
A függőséget megkülönböztethetőnek nevezzük, ha f '(x) van definiálva. A származék megtalálását differenciálásnak nevezzük. Az f '(x) kiszámításához és az f' (x) elemi f (x) -hez való illesztésének szabályait az alábbi táblázat tartalmazza
A származtatott funkció is működik
Minden függőségnek vannak bizonyos tulajdonságai, ezek megismerésével és felfedezésével elemezheti az állapot természetét és a változásokat f (x).
Főbb tulajdonságok:
- Meghatározás és értékrés adatok.
- Nulla f (x)
- A funkció bizonyos intervallumokban növekszik vagy csökken.
- Mutatja a MAX és MIN funkciókat, van-e fordulás.
- Páratlan vagy páratlan f (x)
- Korlátozott és korlátlan funkció.
- Van-e aszimptóta?.
- F (x) frekvencia.

Funkciók és származékok
A függőség jellemzõinek a derivált alkalmazásával történõ megállapításakor az f '(x) tulajdonságok összekapcsolódását az f (x) tulajdonságokkal és fordítva. Az f '(x) karakterisztikákat könnyen meg lehet határozni a függvény gráfon, és fordítva: az f (x) primer karakterisztikáit az f' (x) gráfból kell megérteni. A függvény minden tulajdonságának lényegét meghatározva vizsgálja meg és hozza létre a kapcsolatok láncát. Az aszimptoták grafikonon történő meghatározásához a korlátok fogalmát kell használni..
Az alábbiakban felsorolunk néhány f '(x) és f (x) függvényt:
- Amint f (x) növekszik az intervallumban, f '(x) pozitív.
- Ha f (x) csökken az intervallumon belül, akkor f '(x) negatív.
- F (x) jelenlétében a MAX, f '(x) = 0 pontot nem lehet meghatározni, és az érintőszög tg értéke + értékről jelre változik -.
- F (x) jelenlétében a MIN, f '(x) = 0 pontot nem lehet meghatározni, és az érintõ érintõszögének tg-je megváltozik - és +.
- Amikor f (x) -et hajlítják E-ben, az f '(x) érték nem változtatta meg a jelet a ponton, f' (x) = 0.
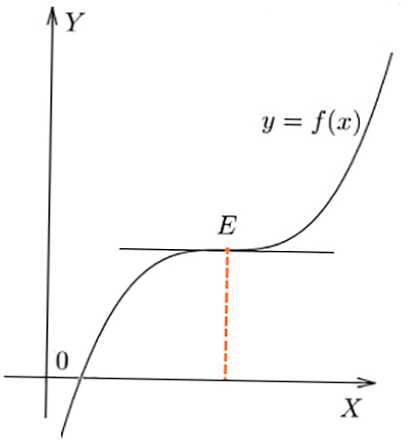
Inflexió a függvénydiagram E pontjában
Kutatás céljából az f (x) egy olyan sémát alkot, amelyben minden egyes lépést egy adott algoritmus szerint készítenek az alkotóelemek kapcsolatának kiszámításához és elemzéséhez.
Funkcionális és derivált különbségek
Az f (x) összeadás és kivonás szabályai megegyeznek a differenciálás során ezen műveletek szabályaival. De az f '(x) megállapításának szabályai a szorzás és a funkciómegosztás műveletei között eltérnek (mint a táblázatban)..
A függvény elsődleges, és a derivált másodlagos matematikai művelet, a legtöbb esetben eltérő tulajdonságokkal rendelkeznek.
A folyamatos függőség inflációs pontját a második deriváltja határozza meg, az előjelének meg kell változnia az x0 pont tartományában.
Vannak olyan típusú függvények, amelyeknek nem van f '(x) az x0 ponton (folytonos). Kifejezésként ln (| x | -1) a származékot nem definiáljuk az x0 = 1 ponton.
Vannak kifejezések "Modulo" hasonlóan y = | x | -hoz, amelynek törése x0-ban van.
Az ilyen függőségekhez csak részben (a meghatározási tartomány intervallumaiban) használják tulajdonságaik tanulmányozását származékokkal, és nem mindig lehetséges az f '(x) tulajdonságokról az elsődleges tulajdonságokra váltani..
A szabályok alóli kivételek nélkül, és még a matematikában sem tehetjük meg. A bemutatott anyag elemzéséhez és konszolidációjához elengedhetetlen példák megoldása, gyakorlat, tapasztalatok megszerzése limitekkel, differenciálokkal és származékokkal, valamint merész lépés az integrálokon.











